1900-luvun kaksi merkittävintä teoreettisen fysiikan pilaria ovat yleinen suhteellisuusteoria sekä kvanttikenttäteoria. Vuosikymmenien ajan näiden pilarien alle yritettiin sovittaa yhteistä jalustaa, kaikki luonnonvoimat sisällään pitävää yhtenäisteorian. Vuosisadan lopussa muotoutui uusi lähestymistapa, vastaavuus kvanttikenttäteorian ja painovoimateorian välillä nk. gauge/gravity -dualiteetti [1]. Tämä vastaavuus auttaa näkemään nämä kaksi perustavanlaatuisesti eri materiaaleista kasattua pilaria saman fysiikan eri ilmentyminä. Ajatusmalli poikkeaa täysin aiemmasta mallista, jossa kaikki luonnonvoimat voitaisiin kuvata yhden yhtenäisteorian turvin.

Gauge/gravity -dualiteetin perusajatus on se, että kvanttikenttäteoriat voidaan muotoilla vaihtoehtoisesti kvanttipainovoiman teorioina. Yksi gauge/gravity -dualiteetin omituisuuksista on se, että kvanttikenttäteoria sekä painovoimateoria elävät paitsi eri aika-avaruuksissa myös vieläpä eri ulottuvuuksissa.  Nämä aika-avaruudet eivät kuitenkaan ole täysin riippumattomat. Tämänhetkisen ymmärryksen mukaan kvanttikenttäteoria eläisi painovoimateorian asuttaman aika-avaruuden reunalla. Tästä syystä gauge/gravity -dualiteettia kutsutaankin useasti holografiseksi dualiteetiksi. Holografia kertoo kuinka korkeampiulotteinen painovoimavuorovaikutus on kudottu kvanttikenttäteorian ilmiömaailmaan, aivan kuin kolmiulotteinen hologrammi voidaan optisesti rekonstruoida kaksiulotteiselta kankaalta.

Kvanttikenttäteorioita on ääretön määrä. Hyvästä syystä yksi tunnetuimmista näistä on hiukkasfysiikan Standardimalli, joka on luonnon tarkka kuvailu korkeimpiin hiukkaskiihdyttimissä testattuihin energioihin asti. Painovoimavuorovaikutuksen välittäjähiukkanen, gravitoni, voi kytkeä materiahiukkasiin monin eri tavoin. Työ säieteorian parissa on opettanut, että matemaattisesti ristiriidattomia tapoja rakentaa kvanttipainovoimateoria on myöskin rajaton määrä. Gauge/gravity -dualiteetin vastaavuus ei kuitenkaan kerro, että mikä tahansa kvanttikenttäteoria voidaan muotoilla kvanttipainovoimateorian sävelin, mutta että sisäisesti ristiriidattomat kvanttipainovoimateoriat ovat itseasiassa piileviä kvanttikenttäteorioita.

On osoittautunut, että hiukkasfysiikan ilmiöiden tarkastelu käyttäen holografista dualiteettia on ollut erittäin palkitsevaa, vaikka tällöin päädytäänkin korkeampiulotteisten maailmojen pariin.  Ehkä tässä vaiheessa onkin hyvä muistaa, että taitavan fyysikon tuleekin osata tehdä hyviä approksimaatioita. Joskus eteen tulee fysiikan ongelmia, jotka ratkeavat analyyttisesti, mutta tämä on ennemminkin poikkeuksellista. Tyypillisesti joudummekin turvautumaan jonkinasteiseen häiriöteoreettiseen menetelmään. Erityisen ansiokas esimerkki tästä on polkuintegraalien Feynmanin diagrammiekspansio, jota Fysiikan tutkimuslaitoksessakin on ansiokkaasti kehitelty vuosien mittaan.

Joskus vastaan tulevan fysiikan ongelman parhainkaan kuvailu ei taivu häiriöteoreettiseksi, tyypillisesti tilanteissa, joissa vuorovaikutuksia kuvaava kytkinvakio on pienen sijaan kertalukua yksi tai jopa suurempi. Tämä ei sinänsä ole teorian ongelma, ongelmaksi muodostuu itse teorian ratkaiseminen. Esim. kvanttiväridynamiikka (QCD) on mitä mainioin teoria vahvojen vuorovaikutuksien kuvailuun korkeilla energioilla, mutta kvarkkien värivankeuden matemaattinen osoittaminen matalilla energioilla on teknisesti hyvin monimutkaista juurikin QCD:n kytkinvakion kasvaessa suureksi.

Tässä päästäänkin holografisen dualiteetin käyttökelpoisimpaan alueeseen: kun toinen teorioista on heikosti vuorovaikuttava, duaalinen teoria on suuren kytkennän alueessa. Valitettavasti tämä ei ole kuitenkaan kaksisuuntainen tie, sillä, jos teoria on vahvasti kytketty, niin siitä ei suoraan pysty päättelemään, että duaalinen kuvailu olisi heikosti kytketty. QCD:n vahvojen vuorovaikutuksien ilmiömaailmaa onnistumme kuitenkin tarkastelemaan heikosti vuorovaikuttavan duaalin avulla.

Jos olemme kiinnostuneet kvanttipainovoimateoriasta, niin holografisen dualiteetin avulla pystymme tutkimaan sitä myös sen alueen ulkopuolella, joka meillä on hallinnassa. Vastaavasti, jos olemme kvanttikenttäteoreetikkoja, duaalisen painovoimateorian avulla pystymme vastamaan kysymyksiin, jotka ovat häiriöteoreettisen tarkastelumme tavoittamattomissa. Vaikka reaalimaailman QCD:n duaalia ei vielä tunneta, on holografia erittäin käyttökelpoinen työkalu. Itseasiassa jo yksinkertaisin duaalimalli joka kuvaa ns. konformaalista suuren värien määrän supersymmetristä Yang-Mills teoriaa on tuottanut uutta kvalitatiivista ymmärrystä raskasionitörmäyksien fysiikasta. Edistyneemmät QCD-mallit, joita Fysiikan tutkimuslaitoksen tutkijatkin ovat kehittäneet, ovat sopusoinnussa lähes kaiken tunnetun QCD-fysiikan kanssa.

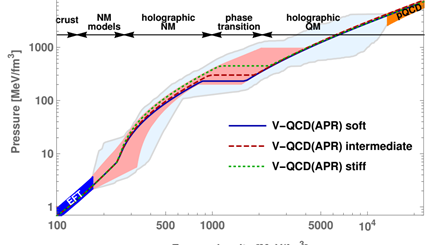
Periaatteellisella tasolla hilatutkijat voisivat ratkaista QCD:n myös siinä alueessa, jossa häiriöteoria ei toimi ja meillä ei näin olisi välttämättä tarvetta holografiselle lähestymistavalle. Käytännössä kuitenkin hilalähestymistapa ei tällä hetkellä sovellu lainkaan dynaamisiin prosesseihin kuten esimerkiksi raskasionitörmäyksiin tai kun aineen tiheys on suuri eli ydinaineen kuvailuun. Holografisilla malleilla tällaisia teknisiä rajoitteita ei ole ja Helsingin ryhmä onkin ollut uraauurtavassa asemassa näiden duaalitekniikoiden soveltamisessa mm. neutronitähtien kontekstissa. Kiinnostunut lukija voi tutustua aiheeseen lisää hiljattain valmistuneesta kirjallisuuskatsauksesta [2].

Muita holografian sovelluskohteita, joita Helsingissä on tutkittu lähiaikoina ovat kvantti-informaatioon liittyvät kysymykset (mm. lomittuminen), useat kiinteän aineen ilmiöt (kvantti-Hall-ilmiö, kummalliset metallit, spontaani symmetriarikko) sekä gravitaatioaaltojen tuotto varhaisen maailmankaikkeuden faasitransitioissa. Näistä kertominen jääköön kuitenkin toiseen kertaan.

Holografia on opettanut, että yleinen suhteellisuusteoria ja kvanttikenttäteoria ovat kuin kolikon kääntöpuolet. Kolikkoa, jonka kääntöpuolelle on lyöty QCD on syytä kuitenkin etsiä huolella [3].

Niko Jokela
vanhempi tutkija, HIP-projekti (High Energy Phenomenology in the LHC era)
Fysiikan tutkimuslaitos

[1] A.V. Ramallo, “Introduction to the AdS/CFT correspondence,” arXiv:1310.4319
[2] C. Hoyos, N. Jokela, ja A. Vuorinen, “Holographic approach to compact stars and their binary mergers,”  arXiv:2112.08422
[3] Linkki historianet.fi sivustolle:  Fyysikko Isaac Newtonista tuli rahanväärentäjien kauhu